저번 포스팅에 시간복잡도가 무엇인지 얘기만 하다 끝났었는데, 이번엔 마지막에 썼던 O(n^2)가 무엇을 의미하는지 알아볼 것이다.
그러기 위해서 우선 점근적 분석 Asymptotic Analysis을 알아야 한다.

점근적 분석이란, 알고리즘에서 우리가 입력하는 크기가 점점 커짐에 따라 성장률을 평가하는 것이다.
이러한 알고리즘들의 성장률을 분석할 때, 우린 어느정도의 입력값을 사용해야 할 지 세부적으로 알기 힘들다.
하지만 아주 큰 값 n으로 근사시켜서 극단적인 경우의 수를 비교하면 오히려 비교가 쉬워진다.

이건 방금 본 그래프에서 함수들을 더 비교하기 쉽게 나타낸 것이다. 뭔가 더 직관적이라 가져왔다. 그냥 함수의 기울기에 따라 비교한 것이다.

이 그래프를 요약하자면,
상수가 가장 느리고 , 가파른 기울기를 가진 지수함수가 가장 빠르다.
전 포스팅에서 근사했던 알고리즘의 시간복잡도를 이런 방식으로 어떤 알고리즘이 더 빠른가 비교할 수 있다.
이렇게 근사하는 방식은 앞에서 표현했던 Big-O 한가지만 있는 것이 아니다.
O - notation (Big-Oh): 더 작거나 같은 관계
o - notation (Little-Oh): 더 작은 관계
Ω - notation (Big-Omega): 더 크거나 같은 관계
ω - notation (Little-Omega): 더 큰 관계
Θ - notation (Big-Theta): 서로 동등한 관계
우선 O - notation (Big-Oh) 먼저 알아보자. 갈 길이 멀다..
Big-Oh
양수인 상수 c와 n이 존재해서 f(n)을 만족할 때, 0 ≤ f(n) ≤ cg(n) 이 식이 성립하면 O(g(n)) 이라 한다.

여기서 짚어야 할 것이 있는데, 우리는 앞으로 나올 예시에서 n0 이전까진 우리가 상관할 바가 아니다. n0이후부터의 n을 가정한다.
아무튼 위의 정의처럼 빅 오를 만족하는 경우, 모든 n에서 f(n)은 c * g(n)보다 작거나 같다고 한다.
즉, f(n) = O(g(n)) 을 근사하여 f(n) ≤ g(n) 으로 표현할 수 있다는 것이다.
여기서 g(n)은 f(n)의 상한 점근선을 갖는다고 말한다.
예를 들어보자.
양수인 상수 c와 n이 존재할 때 7n + 3 ≤ cn 을 만족한다면, f(n) = 7n + 3 = O(n)이라 한다.

함수 f(n)은 안에 어떤 수를 넣어도 g(n)보다 클 수 없다.
그럼 이렇게 말할 수도 있다. 저 f(n)에서 n인것보다 n^2을 넣어도 성립하지 않을까?
7n + 3 ≤ O(n^2) ?? 그럼 7n + 3 = c * n^2인데 양변을 n^2로 나눠보자.
7/n + 3/n^2 ≤ c ??
만약 n이 1보다 크고 c가 4보다 큰 경우, f(n) = O(n^2)를 만족하긴 한다. 그런데 이걸 과연 항상 만족하는 상한 점근선이라 말할 수 있을까? 최고 차수를 나눠서 분수가 되면 이러한 이유때문에 오류가 발생한다. 왜 n^2은 안됐는지 기억하자.
Little-Oh
big 말고 little이 들어갔는데, 이건 상한선이 딱 맞는 점근선이 아님을 의미한다.
이것의 정의는 양수인 상수 c와 n이 존재해서 f(n)을 만족할 때, 0 ≤ f(n) < cg(n) 이 식이 성립하면 o(g(n)) 이라 한다.
f(n) < c * g(n)부분에서 등호가 사라졌다!!
원래 f(n)은 같거나 작았는데 이젠 그냥 c * g(n)보다 작은것이다.
여기선, f(n) = o(g(n)) 을 근사하여 f(n) < g(n) 으로 표현할 수 있다는 의미를 갖는다.
big과 little을 비교해보자면,
big은 몇몇 양수인 상수에 대해 성립하지만 0 ≤ f(n) ≤ cg(n)
little은 모든 양수인 상수에 대해 성립한다. 0 ≤ f(n) < cg(n)
아직 잘 와닿지 않을 수 있다. 몇몇 예시를 보자.
흔히 "Asymptotically tight"하다는 Big-O는, 두 함수나 알고리즘이 같은 순서의 증가율을 갖고 상수 요소의 차이만큼 다를 때 사용된다. 즉, 큰 입력값에 대해 두 함수나 알고리즘이 거의 동일한 성능을 보이는 경우를 말한다.
예를 들어, 두 함수 f(n)과 g(n)에서
f(n) = n^2 + 3 , g(n) = n^2 + 5 인 경우 아주 큰 n에 대해서 동일한 성능을 가지므로 "Asymptotically tight"하다
"Not Asymptotically tight"한 Little-O는 두 함수나 알고리즘이 서로 다른 성능 특성을 가지고 있거나, 하나의 함수가 다른 함수의 성능을 무조건 제한하지 않는 경우를 의미한다.(상한선의 기능이 없는 경우) 즉, 두 함수나 알고리즘이 큰 입력값에서 상당히 다른 성능을 보이거나, 한 함수의 성능이 다른 함수의 성능을 제한하지 않는 경우에 해당된다.
예를 들어, 두 함수 f(n)과 g(n)에서
f(n) = n^2 , g(n) = n^3 인 경우 g(n)이 훨씬 더 빠르기 때문에 f(n)의 성장 속도를 제한하지 않는다. 따라서 "Not Asymptotically tight"하다고 말한다.

Big-Omega
양수인 상수 c와 n이 존재해서 f(n)을 만족할 때, 0 ≤ cg(n) ≤ f(n) 이 식이 성립하면 Ω(g(n)) 이라 한다.

f(n) 과 c * g(n) 순서가 바뀌었다!
이제 f(n)은 c * g(n)보다 크거나 같다.
여기선, f(n) = Ω(g(n)) 을 근사하여 f(n) ≥ g(n) 으로 표현할 수 있다는 의미를 갖는다.
그리고 g(n)은 f(n)의 하한 점근선을 갖는다고 말한다.
예를 들어보자.
f(n) = 3n^2 + 4n + 1 = Ω(n) 임을 보이기 위해
3n^2 + 4n + 1 ≥ cn 에서 전체 식을 n으로 나눠보자.
3n + 4 + 1/n ≥ c
이 식은 2보다 큰 n과 c에서 성립하지 않으므로? 하한을 만족한다!!!!
즉, f(n)의 성장률이 Ω(n)보다 빠르거나 같음을 증명했다. 그러므로 f(n) = Ω(n) 를 성립한다.
Little-Omega
이번엔 하한선이 not asymptotically tight한 little omega이다.
이것의 정의는 양수인 상수 c와 n이 존재해서 f(n)을 만족할 때, 0 ≤ cg(n) < f(n) 이 식이 성립하면 ω(g(n)) 이라 한다.
역시 등호가 사라졌다.
여기선, f(n) = ω(g(n)) 을 근사하여 f(n) > g(n) 으로 표현할 수 있다는 의미를 갖는다.
big과 little을 비교해보자면,
big은 몇몇 양수인 상수에 대해 성립하지만 0 ≤ cg(n) ≤ f(n)
little은 모든 양수인 상수에 대해 성립한다. 0 ≤ cg(n) < f(n)

little-O랑 비교 이미지

Big-Theta
양수인 상수 c1과 c2, n이 존재해서 f(n)을 만족할 때, 0 ≤ c1g(n) ≤ f(n) ≤ c2g(n) 이 식이 성립하면 Θ(g(n))이라 한다.
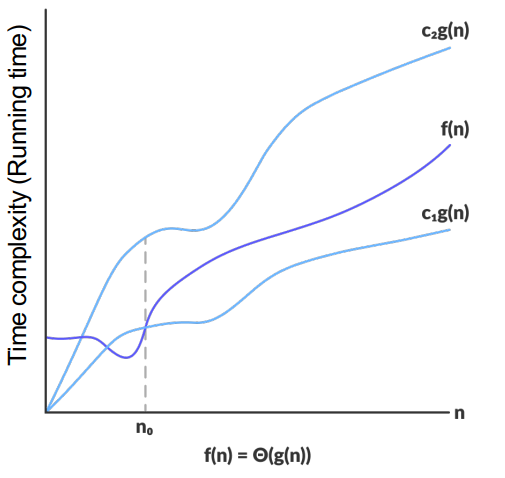
상수 c2가 추가되었다.
이제 f(n)은 c1 * g(n)보다 크거나 같고, c2 * g(n)보다 작거나 같다.
여기선, f(n) = Θ(g(n)) 을 근사하여 f(n) = g(n) 으로 표현할 수 있다는 의미를 갖는다.
그리고 g(n)은 f(n)의 점근선을 갖는다고 말한다. (이제 그냥 점근선이네?)
예를 들어보자.
f(n) = 2n^2 - 3n = Θ(n^2) 임을 보이기 위해
c1n^2 ≤ 2n^2 - 3n ≤ c2n^2 에서 전체 식을 n^2으로 나눠보자.
c1 ≤ 2 - 3/n ≤ c2
각자 특정 조건이 충족될 때 부등식이 성립하므로, 함수의 상한과 하한을 동시에 보여준다. 즉, 주어진 함수가 다른 함수와 동일한 성장률을 가진다는 것을 의미한다.
솔직히 말이 어렵고 복잡하다. 단순하게 함수에서 계수 떼고, 최고차항만 보자는 의미이다. 상한 하한 다 만족하면 세타로 최고차항만 보자~ 이런 말이다.
요약하자면
- f(n) = O(g(n)) 을 근사하여 f(n) ≤ g(n)
- f(n) = o(g(n)) 을 근사하여 f(n) < g(n)
- f(n) = Ω(g(n)) 을 근사하여 f(n) ≥ g(n)
- f(n) = ω(g(n)) 을 근사하여 f(n) > g(n)
- f(n) = Θ(g(n)) 을 근사하여 f(n) = g(n)
그럼 이제 점근 표기법의 예시를 들어보자.



와~ 드디어 정리 끝났다. 하다보니까 참...숨이 막힌다 켁켁
이렇게 많은 점근표기법들을 배웠는데.. 이거 진짜 다 쓰는거 맞나?
사실 빅 오 표기만 쓰는것 같긴 한데.......
그래도 유용하긴 했으니..뭐.. 시험에 안나올건 알지만..... 너무 주절댄다. 끝.
'ps > 자료구조, 알고리즘' 카테고리의 다른 글
| Quick sort 소개 (0) | 2024.04.05 |
|---|---|
| 왜 두 알고리즘을 합친 MergeInsert sort 를 사용해야 할까 (c구현) (0) | 2024.04.05 |
| Divide and Conquer의 재귀문제를 공식으로 풀기 (0) | 2024.03.26 |
| Insertion sort, merge sort 소개와 시간복잡도 구하기 (c구현) (0) | 2024.03.21 |
| Sorting Algorithm과 시간복잡도 개요 (0) | 2024.03.17 |


