AES
AES(Advanced Encryption Standard)는 현재 가장 널리 사용되는 대칭 암호화 알고리즘 중 하나다.
이름에서부터 살짝 눈치챘듯이, 저번 포스팅에서 다뤘던 DES를 대체하는 알고리즘이며 128, 192, 256 비트 중 하나의 키를 선택하여 데이터를 암호화 및 복호화한다.
이러한 다양한 key size 중에서 128비트 key가 가장 널리 사용된다.

물론 각 bit size마다 필요한 round의 수가 다르고, 암호화 과정에서 substitution 및 permutation을 사용한다.
(참고로 DES의 bit size는 64, key size는 56, round는 16라운드까지 있으며 feistal 구조를 사용한다.)
우리는 3가지 bit size 중 가장 널리 사용되는 128bit key size를 기준으로 배워보자.
이와같은 key들은 4 X 4 행렬에 16진수로 표현되어 저장된다.
(128bit를 4 by 4 행렬 공간 16으로 나누면 8. 행렬 한 칸에 8개의 bit가 들어가므로 16진수 2개를 넣을 수 있다 )

예를 들어 첫 번째 칸의 EA는 10진수로 표현하면 14 , 10이다.
이것을 비트로 표현하면 1110 1010 이렇게 8개의 bit로 나타낼 수 있다.
이제 전체적인 구조에 대해 알아보자.

위의 128 bit key size는 10개의 라운드가 있고, 각 라운드마다 Substitute, Shift rows, Mix columns, Add round key가 있다.
특이한 점은 마지막 라운드엔 Mix columns이 없다는 것과, Encryption과 Decryption의 라운드에서 추가되는 round key는 서로 반비례하여 대응된다는 것이다.
이제 각 라운드에 있는 구성 요소들을 알아보자.
우선, Substitute byte 부분은 아까 말한 4 X 4 행렬에 들어온 round key들을 S - box를 사용해서 행렬 블록을 바이트 단위로 치환한다. ( 모든 라운드 substitution )

다음으로 Shift rows 단계는 그냥 행과 행을 단순히 교체한다.( 모든 라운드 permutation )
Mix columns 는 열에 있는 모든 바이트 단위의 함수로 열의 각 바이트를 변경하는 치환을 한다. ( 1에서 9 라운드까지만)
AddRoundKey 단계에서는 현재 상태와 해당 라운드의 라운드 키를 XOR 연산하여 새로운 상태를 생성한다.
초기 라운드에서는 키 스케줄링 알고리즘에 의해 원본 키에서 라운드 키가 생성된다.
이후의 각 라운드에서는 이전 라운드의 라운드 키를 사용하여 새로운 라운드 키가 생성된다.
이제 본격적으로 알아보기 전에... 먼저 알아야 할 수학적 개념들이 필요하다.
사전 수학 개념 - Euclidean Algorithm 과정
일단 간단하게, 유한 field F는 더하기 빼기 곱셈 나눗셈 연산을 갖는 집합이다. 당연히 결합, 교환법칙이 성립한다.
필드에는 실수와 복소수를 포함하지만 정수는 포함하지 않는다.
뭐 이런 조건이 있나 했는데, 정수 집합은 덧셈과 곱셈에 대한 모든 규칙을 만족하지는 않기 때문이었다.
예를 들어, 정수 집합에는 모든 원소에 대해 곱셈의 역원이 존재하지 않는다. 또는 0으로 정수를 나눌 경우 정의되지 않음.
첫 번째로 Zp = {0, 1, ... , p-1} 는 p가 소수라면 필드라는 개념과
GF(p^n)은 각각의 원소가 p^n개 만큼 가능한 값을 가질 수 있는 수(필드) 개념이 있다.
여기서 GF는 Galois Field의 약자로, 유한체를 나타내는 용어이다.
유한체는 유한 개수의 원소로 이루어진 수학적인 구조를 갖는다. 주로 덧셈과 곱셈의 mod 연산을 한다.
예시

글씨가 많이 개판이긴 한데,,,
결과 먼저 말하자면 이 다항식 P(X)를 2차식들의 곱으로 나타낼 수 없다는 것을 의미한다.
( P(X) = X^8 + X^4 + X^3 + X + 1 는 Z2[X]에서 나눌 수 없다 )
Z2[X]에서의 다항식은 이항계수가 2인 유한체(또는 이항체) 상의 다항식을 의미한다.
Z2[X]가 0과 1로 이루어진 유한체이며, 연산은 모듈로 2 연산으로 정의된다는 말이다.
그냥 XOR 비트 연산으로 이해하자.
아무튼, 이 말은 다항식이 더 작은 차수의 다항식들의 곱으로 나타낼 수 없음을 의미한다.
솔직히 이해가 잘 되는 편은 아니다. 그냥 바이너리 필드를 생성해서 XOR연산을 하기 위한 빌드업 떡밥이었구나 생각하자.
그리고 GF(2^8)이 의미하는 것은 7차 이하의 다항식으로 이루어졌다고 말하는 것이다.
물론 각 차수의 계수는 0 아니면 1이다.
좀 더 글씨를 성의있게 신경쓴 덧셈 곱셈 예시를 보자.
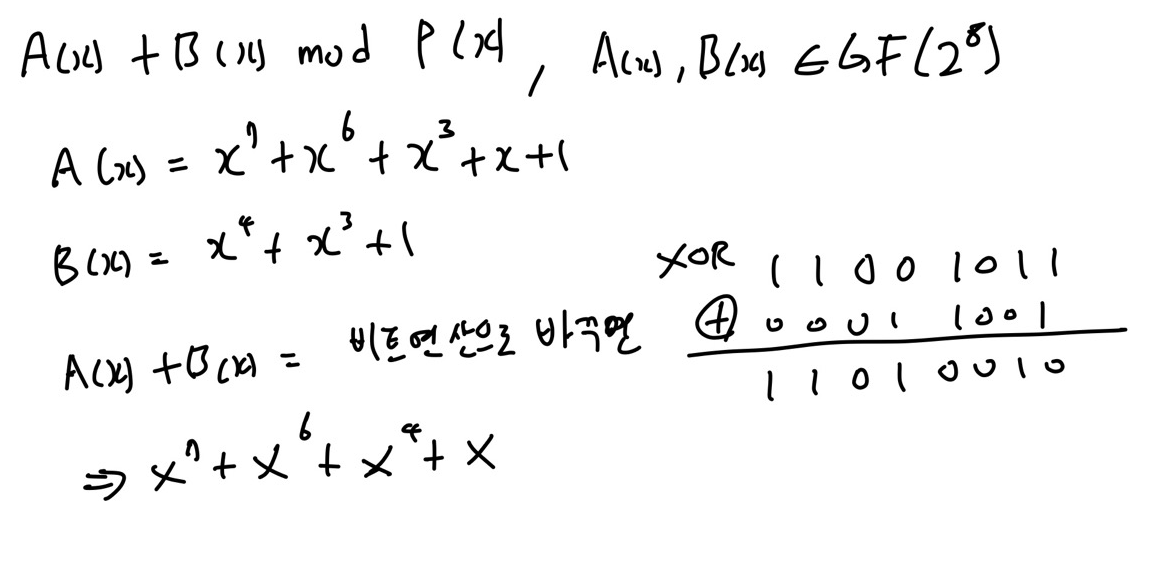
이런 느낌으로 덧셈은 각 차수의 계수만 떼어내어 XOR 연산을 하면 된다.

두 다항식을 곱하고 나면 mod에 있는 P(x) 다항식보다 커지는 경우가 있다.
이 때, 다항식을 mod 다항식으로 나눠주면 된다. 나눠주는 방식에는 이와 같은 두 가지의 방식이 있다.
1번은 그냥 나누면 되는거고.. 2번은.. 이런 XOR방법도 있다고 한다. 나중에 mix column 단계에서 사용한다고 한다.
이제 나눗셈 과정을 알아보기 위해 먼저 역수를 구하는 예시를 보자. 역시 지금봐도 글씨가 좀 그렇긴 하네

좀 더 성의있게 쓴 Euclidean Algorithm 참고
위 이미지의 나눗셈에서 나머지를 자꾸 다시 좌변으로 옮기고 옮기고.. 반복하는 이 과정을 저기 써놓은대로 Euclidean Algorithm이라 한다.
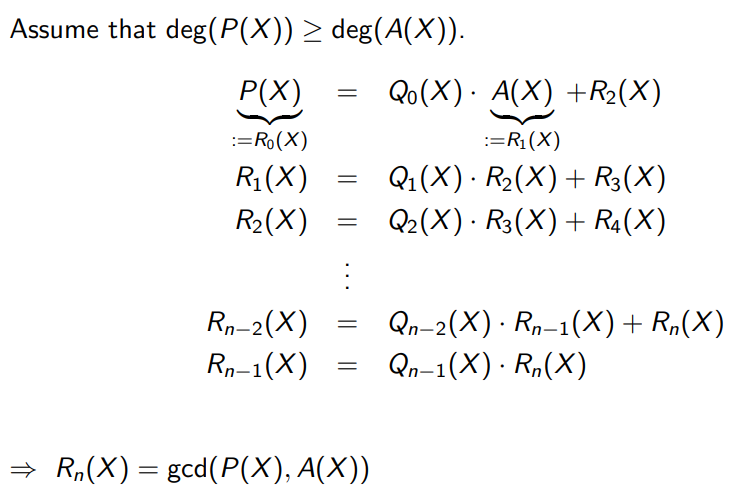
이걸로 gcd를 구할 준비를 마쳤다.
아래는 그냥 Euclidean Algorithm 예시로 주어진 것이다.
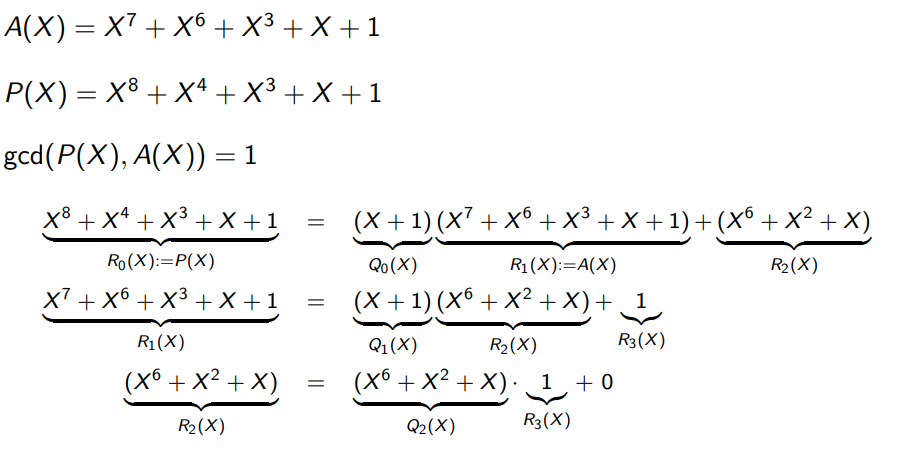
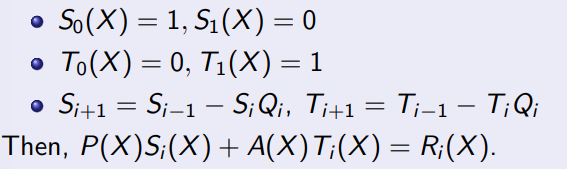
이건 Extended Euclidean Algorithm의 이론이다.
아래는 이것을 사용한 예시
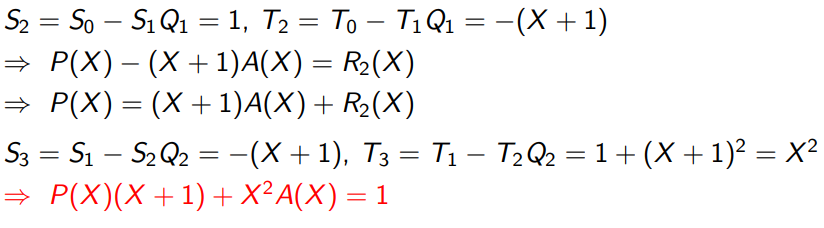
이건 affine 암호에서 설명했던 것과 같이, 역수를 구하기 위해 뭐 이런 연산 과정이 있다는 것을 보여줬다.
간단하게 정리하면
Euclidean Algorithm과 extend Euclidean Algorithm 과정을 보여주기 위한 예시였다.
솔직히 Euclidean 쓰기보다 그냥 하나씩 때려맞추는게 더 빠르다고 한다. (교수님 오피셜)
아무튼 이제 식 A(x)가 주어졌을 때, A(x)의 역수 mod P(x)를 구해보자.
참고로 gcd(A(x), P(x)) = 1 을 구하는 것에서 시작한다. (A가 P의 곱이 아닌 경우 gcd = 1이 성립한다.)
그리고 P(x), A(x)와 똑같이 필드에 속하는 임의의 다항식 T(x), A(x)이 존재할 때
P(X)S(X) + A(X)T(X) = gcd(P(X), A(X)) = 1가 성립한다.
그러면 A(X)T(X) ≡ 1 (mod P(X)) 이란 소리고,
T(X) ≡ A(X) ^(−1) (mod P(X)) 이와 같은 식을 얻을 수 있다. (이것들을 Euclidean Algorithm이라 함)
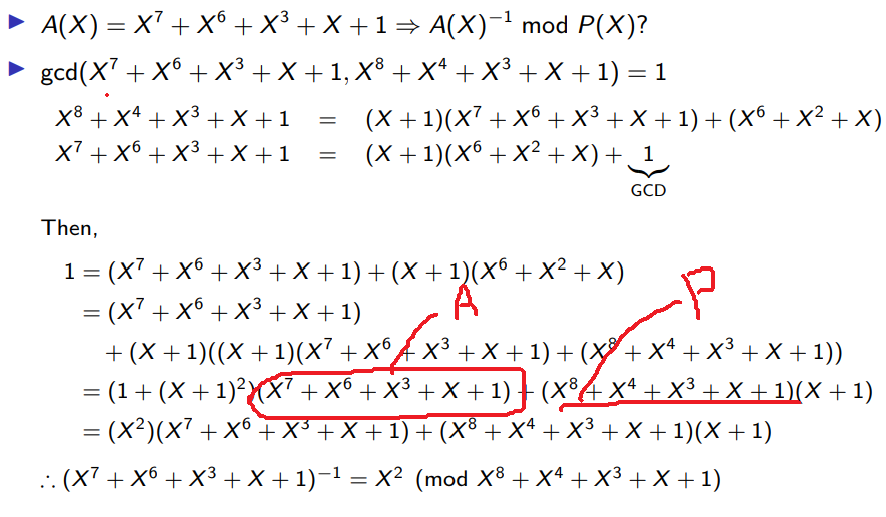
이 식이 좀 복잡해 보이기는 한데, mod2 연산에서 뺄셈을 덧셈으로 바꿔줄 수 있다는 것을 유의하고 식을 엄청 대입하다보면 풀리기는 한다. (이게 Extended Euclidean Algorithm )
위에 Z26 쪽을 다시 보면, 15*ㅁ + 26 *ㅁ = 1 부분에서 우리가 구할 것은 15의 역수부분이지 26은 뭐가 되어도 상관없었다. 그런 논리로 우리는 X^2 를 얻을 수 있다.
이 과정을 아래에 어떻게 좀.. 풀어서 쓰긴 했는데..

ㅋㅋ
아무튼 드디어 AES를 공부할 수학적 지식 기초가 끝났다.
S-box를 이용한 substitute
다시 AES로 돌아와서
16진수로 나타낸 AES의 S-box S(xy) 는 (x, y)로 행과 열을 나타낸다. S-box와 그 inverse table을 보면 서로 대응되는 것을 확인할 수 있다.
S-box와 inverse table 예시)
아까 4 X 4행렬의 round key 를 S-box에 대입해서 치환해준다.
저기 접은글에 있는 S-box대로 예시를 들어보자면

이런 식으로 변환된다.
이제 최종적으로 S-box 연산의 과정에 대해 알아보자.
아까 다항식의 계수만 뽑아내서 이진수로 계산했던 과정을 기억해보자.
예를들어 그 계수만 뽑아낸 {x7,x6,...x0}이 있다고 치자. 이 계수들의 역수를 구해서 다시 {y7,y6,...y0}을 구한다. 한마디로, x의 역수가 y이다.
이렇게 구한 y들에 행렬곱과 덧셈을 해줘서 최종적으로 z를 구하여 암호화한다.

shift row
S-box를 이용한 substitute 과정은 지나갔으니, 다음으로 shift row를 알아보자.

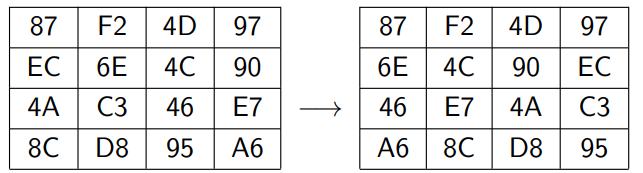
첫 번째 행은 움직이지 않는다.
두 번째 행은 1 byte 만큼 왼쪽으로 shift된다.
세 번째 행은 2 byte 만큼 왼쪽으로 shift된다.
네 번째 행은 3 byte 만큼 왼쪽으로 shift된다.
byte 단위로 이동이 이루어지다 보니, 각 byte 안의 bit 순서는 변하지 않는다.
Mix Columns
각각의 열 단위를 미리 정의된 행렬 M에 곱하여 새로운 열을 생성한다. (M은 비가역적 행렬)
당연하다면 당연한건데, shift row의 연산은 byte단위로 이동했기 때문에 그 안의 bit는 변하지 않았지만 mix columns 연산은 각 열을 행렬 M에 곱하기 때문에 byte안의 bit는 변한다.
예를 들어보자. 아래와 같은 행렬에 Mix Columns 연산을 적용시켜보자.
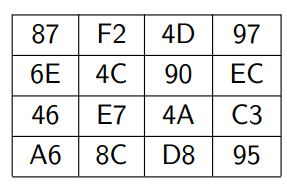
그리고 GF(2^8)의 행렬 M이 있다고 생각해보자.

이 행렬은 다항식으로도 표현 가능하다.
물론 우리가 곱할 행렬의 열들도 다항식으로 표현 가능하다.

이렇게 각 행렬들을 곱하게 되면 Mix column으로 싹 다 변환된 새로운 4 X 4 행렬이 만들어진다.
참고로 위의 열 계산은 0100 0111으로 47이 나온다.
두 번째 열도 계산해보자. 저 수많은 다항식 곱셈을 전부 다 하는게 아니다.
아래와 같이 비트연산으로 바꾼 후 모두 더해주는 것으로 빠르게 계산할 수 있다.

후.. 얼마 안남았다.
Add round key
드디어 마지막 연산, Add round key 변환이다.
위에서 계산한 상태의 128bit를 round key의 128bit와 더해준다.

반대로 add round key의 inverse 연산은
round key의 Output과 round key를 XOR 연산하면 현재 상태의 비트가 나온다.
그런데 이와 같은 각 round key를 생성하기 위해서는 먼저 key expansion을 수행한 후에서야 Add round key 연산을 할 수 있다.
key expansion은 word 4개로 각 round key를 생성한다.
Key K = (W (0), W (1), W (2), W (3))로 표현함.
그러면 10개의 round가 있으니까 40개의 워드가 필요한가 싶지만 1round로 들어가기 전에 round key와 XOR연산을 하기 때문에 1라운드가 더 추가된 44word가 필요하다.

위 표에서 눈치챘겠지만, 계산은 각 열마다 따로 한다.
일단 계산하기 위해서 key expansion은 들어온 128bit의 key를 4개의 워드로 변환한다. (1word가 4byte니까)

그
리고 각 round마다 다음의 연산을 수행한다.

이렇게 DES에서 보다 개선된 AES를 알아봤다.
DES보다 훨씬 큰 key size를 사용하기 때문에 brute force방식으로부터 그나마 더 안전하다.



