명제
- 조건문 (Conditional, →): "p이면 q이다"의 형태로, p가 참이고 q가 거짓일 때만 거짓이 됩니다.

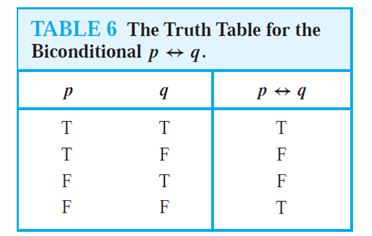
- 쌍방 조건문 (Biconditional, ↔): p와 q가 같은 진리값을 가질 때만 참이 됩니다.
항진명제와 모순명제 (Tautology and Contradiction)
- 항진명제 Tautology : 항상 참인 복합 명제입니다. 예를 들어, "p ∨ ¬p"는 항상 참이므로 항진명제입니다.
- 모순명제 Contradiction : 항상 거짓인 복합 명제입니다. 예를 들어, "p ∧ ¬p"는 항상 거짓이므로 모순명제입니다.
- 임의명제 Contingency : 항진명제도 모순명제도 아닌 명제를 뜻합니다.
논리적 등가 (Logical Equivalence)
- 두 복합 명제 p와 q가 논리적으로 등가라면, p ↔ q가 항상 참이 됩니다. 이를 진리표를 통해 확인할 수 있습니다. 예를 들어, ¬(p ∨ q)와 ¬p ∧ ¬q는 논리적으로 등가입니다.
드모르간 법칙 (De Morgan's Laws)
- 두 명제에 대한 드모르간 법칙은 다음과 같습니다:
- ¬(p ∨ q) ≡ ¬p ∧ ¬q
- ¬(p ∧ q) ≡ ¬p ∨ ¬q
전칭 한정자와 존재 한정자 (Universal and Existential Quantifiers)
- 전칭 한정자 (∀): P(x)가 모든 x에 대해 참이라는 것을 의미합니다. 예를 들어, "모든 실수 x에 대해, x + 1은 x보다 크다"는 진술은 참입니다.
- 존재 한정자 (∃): P(x)가 적어도 하나의 x에 대해 참이라는 것을 의미합니다. 예를 들어, "x > 3"이라는 진술에서 적어도 하나의 실수 x가 3보다 크므로 참입니다.
유일성 한정자 (Uniqueness Quantifier)
- 유일성 한정자 (∃! 또는 ∃1)는 오직 하나의 x에 대해 P(x)가 참임을 의미합니다. 예를 들어, "단 하나의 컴퓨터만이 공격받고 있다"는 진술을 표현할 수 있습니다.
헷갈리는거 응용
¬∀x(P(x) → Q(x)) and ∃x(P(x)∧¬Q(x)) 논리적으로 같다는것 증명하기
- ¬∀x(P(x)→ Q(x))
- ≡∃x(¬(P(x) → Q(x)))
- ≡∃x(¬(¬P(x)∨Q(x)))
- ≡∃x(P(x)∧¬Q(x))

추론 규칙 (Rules of Inference)
- 추론 규칙은 기존 명제로부터 새로운 명제를 유도하는 데 사용됩니다.

증명
- 공리 (Axiom): 참이라고 가정되는 진술.
- 정리 (Theorem): 참이라고 증명된 수학적 진술.
- 명제 (Proposition): 상대적으로 덜 중요한 정리이지만 여전히 중요한 결과.
- 레마 (Lemma): 다른 결과의 증명에 도움이 되는 부차적인 정리.
- 추론 (Corollary): 이미 증명된 정리로부터 직접적으로 도출되는 정리.
직접 증명 (Direct Proofs)
- 직접 증명은 명제 p→q에서 가 참임을 가정하고, 정의나 이미 증명된 정리를 이용하여 q가 참임을 증명하는 방식입니다. 예를 들어, "n이 홀수라면 n2도 홀수다"라는 정리를 직접 증명할 수 있습니다.
간접 증명 (Indirect Proofs)
- 간접 증명은 반대 가정(contrapositive)을 이용하여 p→q를 증명하는 방법입니다. 이 방법에서는 가 거짓일 경우 도 거짓이 된다는 것을 보여줍니다. 예를 들어, "3n + 2가 홀수라면 n도 홀수다"를 간접 증명으로 해결할 수 있습니다.
공허한 증명 (Vacuous Proof)
- 공허한 증명은 가정 p가 거짓임을 보여서 p→q가 참임을 증명하는 방식입니다.
사소한 증명 (Trivial Proof)
- 사소한 증명은 결론 가 항상 참임을 이용하여 p→q를 증명하는 방식입니다. 예를 들어, "a와 b가 0 이상일 때 a≥b"는 사소한 증명으로 해결할 수 있습니다.
간접 귀류법 (Proof by Contradiction)
- 귀류법은 p가 참이라는 것을 증명하기 위해 반대 가정을 하고, 그 가정에서 모순이 도출됨을 보여 가 참임을 증명하는 방법입니다. 예를 들어, "루트 2가 무리수다"라는 명제를 증명할 때 자주 사용됩니다.
등가 정리의 증명 (Proof of Equivalence)
- 등가 정리는 p↔q를 증명하기 위해 p→q와 q→p를 모두 증명하는 방식입니다.
반례 (Counterexample)
- 반례는 "모든 x에 대해 p(x)가 참이다"라는 명제가 거짓임을 보여주는 사례입니다. 예를 들어, "모든 양의 정수는 두 정수의 제곱의 합이다"라는 명제에 대해 3이 반례가 됩니다.
존재 증명 (Existence Proof)
- 존재 증명은 적어도 하나의 가 주어진 조건을 만족함을 보여주는 증명입니다. 이를 구성적 증명이나 비구성적 증명으로 나눌 수 있습니다.
유일성 증명 (Uniqueness Proof)
- 유일성 증명은 특정 조건을 만족하는 유일한 x가 존재함을 증명하는 방식입니다. 예를 들어, "특정 조건을 만족하는 유일한 실수 r이 존재한다"는 것을 증명하는 방식입니다.
집합
멱집합 (Power Set): 집합 의 모든 부분집합들의 집합을 멱집합이라고 하며, P(S)로 표기합니다.
- 예: P(0,1,2)={∅,0,1,2,0,1,1,2,0,2,0,1,2}
- 바닥 함수 ⌊x⌋: 주어진 실수 x보다 작거나 같은 가장 큰 정수를 반환합니다. 즉, x를 내림한 값입니다.
- 천장 함수 ⌈x⌉: 주어진 실수 보다 크거나 같은 가장 작은 정수를 반환합니다. 즉, 를 올림한 값입니다.
알고리즘 종류
탐색 알고리즘 (Searching Algorithms)
- 선형 탐색 (Linear Search): 리스트의 첫 번째 요소부터 순차적으로 비교하여 원하는 값을 찾습니다. 값이 발견될 때까지 탐색을 계속합니다.
- 이진 탐색 (Binary Search): 정렬된 리스트에서 중간 값을 기준으로 리스트를 두 부분으로 나누어 탐색 범위를 좁혀갑니다. 이 방법은 리스트가 정렬되어 있을 때만 사용할 수 있습니다.
버블 정렬 (Bubble Sort): 인접한 두 요소를 비교하여 잘못된 순서일 경우 교환하는 방식으로 정렬합니다. 가장 큰 값이 맨 마지막으로 "버블처럼" 올라갑니다.
- 삽입 정렬 (Insertion Sort): 두 번째 요소부터 시작하여 자신의 위치를 찾아 앞의 요소들과 비교해 정렬된 리스트에 삽입합니다.
탐욕 알고리즘 (Greedy Algorithm)
- 탐욕 알고리즘은 최적화 문제에서 각 단계에서 그 순간 가장 좋은 선택을 하는 방식으로 해를 구합니다. 모든 경우를 고려하지 않고 즉각적인 최적 선택만을 하므로, 항상 최적의 해를 보장하지는 않습니다.
- 예: 동전 문제에서 최소 동전 개수로 거스름돈을 계산하는 방법.
알고리즘 분석 (Algorithm Analysis)
- 알고리즘의 효율성을 비교하기 위해 시간 복잡도와 공간 복잡도를 분석합니다.
- 빅오 표기법 (Big-O Notation): 입력 크기 n에 대한 알고리즘의 성능을 측정하는 데 사용됩니다. f(x)가 O(g(x))일 때, 상수 C와 임계값 가 존재하여 f(x)≤Cg(x)를 만족합니다.
- 예: x^2 + 2x + 1 은 O(x^2)
빅오, 빅오메가, 빅세타 표기법
- 빅오 (Big-O): 상한을 나타냅니다. 어떤 입력에 대해서도 주어진 함수보다 작거나 같은 성능을 보장합니다.
- 빅오메가 (Big-Omega): 하한을 나타냅니다. 어떤 입력에서도 주어진 함수보다 크거나 같은 성능을 보장합니다.
- 빅세타 (Big-Theta): 상한과 하한이 동시에 성립하는 경우를 나타냅니다.

