close
프로필 배경
프로필 로고

학교공부일기장

cs/데이터베이스 · 2024. 10. 14. fullscreen 넓게보기

B-Tree의 insertion과 split 생성 과정

 

B-TREE-SEARCH(x, k):
    i = 1
    while i ≤ x.n and k > x.key_i:
        i = i + 1
    if i ≤ x.n and k == x.key_i:
        return (x, i)
    elif x.leaf:
        return NIL
    else:
        DISK-READ(x.c_i)
        return B-TREE-SEARCH(x.c_i, k)

 

B-트리는 여러 키와 자식을 포함할 수 있으므로 탐색 절차가 이진 트리보다 복잡하다.

위 알고리즘은 트리 구조에서 서브트리를 탐색할 수 있도록 일반화된 형태로 설계한 것이다.

 

 

 

위 설계의 입력부분인 x는 탐색을 시작할 서브트리의 루트 노드를 가리키는 포인터를 의미하고, k는 탐색하고자 하는 키를 의미한다.

 

이에 따라 출력하게 될 return 부분은 키 k가 B 트리에 있다면 정렬된 쌍 (𝑦,𝑖)를 반환하고, 키값을 찾을 수 없다면 NIL를 반환한다.

여기서 y는 키 k가 위치한 노드이고, i는 해당 노드에서 키 k가 위치한 인덱스이다.

 

 

 

 

 

 

B-Tree 탐색 절차 (B-Tree Search Procedure)

  1. Find:
    • 가장 작은 인덱스 를 찾는다.
      k≤x.keyi 를 만족하는 인덱스를 선택해, 탐색할 적절한 자식을 정한다.
  2. Check:
    • 현재 노드에서 우리가 원하는 키를 발견했는지 확인한다.
      키를 발견하면 해당 노드와 인덱스 (x,i) 쌍을 반환한다.
  3. Terminate:
    • 현재 노드가 리프 노드일 경우 탐색을 종료한다. 키가 존재하지 않는다면 NIL을 반환한다.
  4. Recurse:
    • 원하는 키를 찾지 못했다면, 적절한 자식 노드로 이동해 재귀적으로 탐색한다.

 

 

 

 

 

 

B-Tree 탐색 시간 복잡도 (Time Complexity of B-Tree Search)

 

 

  1. 트리의 높이 h:
    • 트리의 높이는 O(log⁡_t n)이다. 여기서 t는 최소 차수이다.
  2. 각 노드의 키 탐색:
    • 각 노드 내에서 키를 찾기 위해 선형 탐색을 수행하며, 이때 각 시간 복잡도는
  3. 총 시간 복잡도:
    • 트리의 높이와 각 노드 내 키 탐색 비용을 곱하면
      B-트리 탐색의 전체 시간 복잡도는 

 

 

 

 

B-Tree의 각 노드에서 선형 탐색 대신 이진 탐색을 적용한다면, 이 경우의 시간 복잡도는 다음과 같다.

  1. 이진 탐색의 시간 복잡도:
    • 이진 탐색은 각 노드에서 O(log ⁡t) 시간에 키를 찾을 수 있다. 여기서 t는 해당 노드의 최대 키 개수
  2. 전체 탐색의 시간 복잡도:
    • 트리의 높이는 h=O(log⁡_t n) 이므로
      이진 탐색을 적용한 전체 탐색의 시간 복잡도는: O(log⁡t⋅log_⁡t n)
  3. 로그 복잡도 변환:
    • 위 식은 로 단순화될 수 있다.
      이것의 의미는 이진 탐색 덕분에 각 노드의 탐색 비용이 크게 줄어들었음을 의미한다.

 

 

결국

  • 선형 탐색을 사용한 기존 B-Tree 탐색: O(t⋅log⁡_t n)
  • 이진 탐색을 사용한 새로운 B-Tree 탐색: O(log⁡ n)

 

 

 

이렇게 각 노드에서 선형 탐색 대신 이진 탐색을 수행하면, 큰 데이터셋에서도 더 빠른 탐색이 가능하다.

특히, 트리의 차수가 매우 큰 경우는 성능 차이가 더 두드러지게 나타난다.

 

 

 

 

 

 

 

B-트리 생성 방법 (How to Build a B-Tree)

 

B-Tree-Create 함수를 통해 빈 루트 노드를 생성하고, 비어있는 B-tree 에 insert로 키를 하나씩 삽입하여 트리를 구성한다.

 

 

 

B-TREE-CREATE(T):
   x = ALLOCATE-NODE()  # 새 노드 할당
   x.leaf = TRUE         # 초기에는 루트가 리프 노드
   x.n = 0               # 현재 키의 개수는 0
   DISK-WRITE(x)         # 노드 정보를 디스크에 기록
   T.root = x            # 트리의 루트로 설정

 

빈 B-tree 생성 과정

  1. 디스크 공간 할당:
    • 새 노드를 위해 디스크 페이지(disk page)를 할당한다.
  2. 노드 속성 설정:
    • x.leaf = TRUE: 새로 생성된 루트 노드는 초기에 리프 노드로 간주한다.
    • x.n = 0: 현재 생성된 노드에는 아직 키가 하나도 포함되어 있지 않다.
  3. 디스크에 노드 정보 저장:
    • DISK-WRITE(x)를 통해 새로 생성한 노드의 정보를 디스크에 기록한다.
  4. 트리의 루트 노드 설정:
    • T.root = x: 새로 생성된 노드를 트리의 루트 노드로 설정한다.

 

 

 

 

 

 

BST(이진 탐색 트리)와 B-트리에서의 키 삽입 차이점

 

 

 

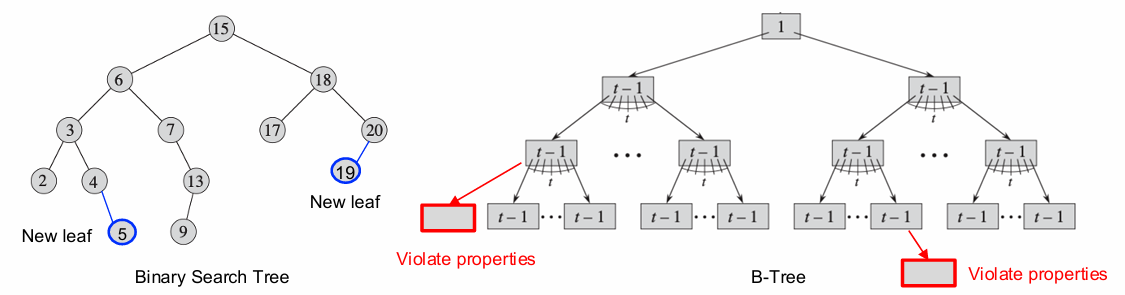
BST (Binary Search Tree)에서의 삽입 과정

  1. 적절한 위치를 탐색하여 새 키를 삽입할 리프 노드를 찾는다.
  2. 새로운 리프 노드를 생성하고 새 키를 삽입한다.
  3. 균형을 유지하기 위해 조정이 필요할 수 있다.

 

리프노드에 추가하기만 하면 된다고 해서 삽입할 때 마구마구 새 리프를 추가하면 트리의 균형이 깨질 수 있다.

그러나 고정된 두 개의 자식 노드를 가진 구조에서 균형을 맞추는 것은 상대적으로 단순하긴 하다.

 

 

 

 

 

B-트리에서의 삽입 과정

 

B-트리는 각 노드에 여러 개의 키와 자식을 포함하므로, BST처럼 단순히 새 리프를 추가하는 방식으로 삽입할 수 없다.

 

B-트리는 모든 노드가 특정 범위의 키 수를 유지해야 하고,

삽입 시 노드가 초과로 가득 차게 되면 B-트리의 속성이 깨질 수 있다.

예를 들어, 한 노드에 너무 많은 키가 들어가면 B-트리의 균형 조건이 위배된다.

그리고 한 노드에 너무 많은 키가 삽입되면 오버플로(overflow)가 발생할 수도 있다..

 

 

 

이런 상황을 예방하기 위한 해결방안은 다음과 같다.

  • 노드가 가득 차면 분할(splitting)을 수행한다.
  • 키를 두 개의 노드로 나누고, 중앙값을 부모 노드로 올리는 방식으로 균형을 유지한다.

 

 

 

결국, BST는 삽입이 단순하지만 균형이 깨질 수 있어 조정이 필요하고

B-트리는 삽입 시 노드가 가득 차는 문제를 해결하기 위해 분할과 조정을 수행하는 것으로 트리의 균형을 유지한다.

 

 

 

 

 

 

Split 연산

 

 

  • 가득 찬 노드 y (최대 2t−1 개의 키 보유)를 중간 키(median key)를 기준으로 두 개의 노드로 나눈다.
  • 중간 키는 부모 노드로 이동한다.
    부모 노드가 가득 찬 경우, 해당 노드도 분할해야 하며 재귀적으로 분할이 발생할 수 있다.

 

 

 

 

B-Tree-Split-Child 과정

 

B-Tree-Split-Child(x, i)
  z = ALLOCATE-NODE()    # 새로운 노드 z 할당
  y = x.c_i              # 가득 찬 자식 노드 y
  z.leaf = y.leaf        # z도 y와 같은 리프 여부 설정
  z.n = t - 1            # z에 t-1개의 키 설정
  for j = 1 to t - 1     
      z.key_j = y.key_{j+t}  # y의 절반 키를 z로 이동
  if not y.leaf
      for j = 1 to t     
          z.c_j = y.c_{j+t}  # y의 자식 포인터를 z로 이동
  y.n = t - 1               # y의 키 수를 t-1로 설정
  for j = x.n + 1 downto i + 1
      x.c_{j+1} = x.c_j    # x의 자식 포인터 이동
  x.c_{i+1} = z            # 새로 생성된 z를 x의 자식으로 설정
  for j = x.n downto i     
      x.key_{j+1} = x.key_j  # x의 키 이동
  x.key_i = y.key_t         # 중간 키를 x로 이동
  x.n = x.n + 1             # x의 키 수 증가
  DISK-WRITE(y)             # y를 디스크에 저장
  DISK-WRITE(z)             # z를 디스크에 저장
  DISK-WRITE(x)             # x를 디스크에 저장

 

1. 노드 z 생성

  • z는 새로운 자식 노드로, y의 절반을 분리하여 생성한다.

 

 

2. 가장 큰 t - 1개의 키를 z로 이동

  • y에서 가장 큰 t - 1개의 키를 z에 복사한다.

 

 

3. 해당하는 자식 노드를 z에 할당

  • 만약 y가 리프 노드가 아닌 경우, y의 자식 노드 중 일부를 z에 할당한다.
    ex) y의 오른쪽에 있던 자식 노드들이 z의 자식 노드가 된다.

이 과정을 Cutting and Pasting (키와 자식 이동) 라고 한다.

 

 

4. y의 키 수 조정

  • y의 키 개수를 2t - 1에서 t - 1로 줄입니다.
    • 이는 y에서 중앙값과 그 이상의 키들을 제거했기 때문에 발생한다.

 

 

5. z를 부모 노드 x의 자식으로 삽입

  • 새로 생성된 노드 z를 부모 노드 x의 자식 노드로 추가한다.
    • x의 자식 노드를 오른쪽으로 한 칸 이동하여 빈 공간을 확보한 뒤 그 자리에 z를 삽입한다.

 

 

6. 중앙 키 S를 y에서 x로 승격

  • y의 중앙 키 S를 x로 올려서 y와 z를 구분하는 경계로 사용하여 트리 구조를 유지한다.

 

 

7. x의 키 수 조정

S가 x로 승격되었기 때문에 x의 키 개수를 1 증가시킨다.

 

 

 

B-Tree-Split-Child 연산은 노드가 가득 찬 경우, 이를 두 개로 나누고 부모 노드로 중간 키를 이동시켜 트리의 균형을 유지했다.

이렇게 트리의 삽입 연산을 효율적으로 처리하며, 트리의 높이 증가를 최소화한 덕분에

B-Tree는 삽입, 삭제, 검색 연산에서 항상 일정한 성능을 유지할 수 있다.

 

 

 

 

 

 

루트가 가득 찬 경우

 

 

  1. 새로운 노드 생성:
    • 루트 노드가 가득 찬 경우, 새로운 노드 를 생성한다.
    • 이 새 노드는 새로운 루트가 되며, 기존 루트를 자식 노드로 가진다.
  2. 루트 노드의 분할:
    • 기존 루트 r을 두 개로 나누고, 중간 키를 새 루트 로 이동한다.
  3. 트리의 높이 증가:
    • 새로운 루트 s가 생기면서 트리의 높이가 1 증가하게 된다.

 

 

 

루트가 가득 차지 않은 경우는 위에서 본 대로 그냥 적절한 자리에 삽입한다.

 

 

B-Tree-Insert(T, k)
  r = T.root               # 루트 노드를 가져옴
  if r.n == 2t - 1         # 루트가 가득 찬 경우
      s = ALLOCATE-NODE()  # 새로운 루트 노드 s 생성
      T.root = s            # s를 트리의 새로운 루트로 설정
      s.leaf = FALSE        # s는 리프가 아님
      s.n = 0               # s의 초기 키 개수는 0
      s.c_1 = r             # 기존 루트를 s의 첫 번째 자식으로 설정
      B-Tree-Split-Child(s, 1) # 루트 분할
      B-Tree-Insert-NonFull(s, k) # 새로운 키 삽입
  else B-Tree-Insert-NonFull(r, k) # 루트가 가득 차지 않은 경우 삽입

 

 

이 경우는 꽤 중요한 요소이다.

트리의 높이가 낮을수록 탐색과 삽입 속도가 빨라지며, 이를 통해 디스크 접근을 최소화하는 데도 기여하는데

B-Tree의 높이 증가는 루트 노드의 분할로만 이루어지기 때문이다.

 

 

그렇다고 정확히 루트 노드만 주의해야 하는 것은 아니다.

B-Tree의 하위 레벨에서 균형을 유지하기 위해 분할이 루트까지 전파될 수 있기 때문이다.

 

 

하지만 이러한 분할이 나쁘다는 것은 아니다.

 

 

B-Tree의 분할은 트리의 상단에서만 일어나므로 트리의 균형과 성능을 보장할 수 있다.

반면 BST는 삽입 순서에 따라 불균형하게 성장할 수 있어, 성능이 저하될 가능성이 크다.

이러한 이유로 B-Tree는 대규모 데이터베이스나 파일 시스템에서 효율적으로 사용되고 있다.

 

 

 

 

 

지금까지 B-Tree에서 가득 찬 노드에 새로운 키를 삽입했었다면, 이제 가득차지 않은 노드에 삽입할 차례이다.

 

def BTreeInsertNonFull(x, k):
    i = x.n  # 현재 노드의 키 개수
    
    # 만약 x가 리프 노드라면
    if x.leaf:
        # 키를 삽입할 위치를 찾는 과정 (오른쪽에서 왼쪽으로 탐색)
        while i >= 1 and k < x.keys[i - 1]:
            x.keys[i] = x.keys[i - 1]
            i -= 1
        x.keys[i] = k  # 새로운 키 삽입
        x.n += 1  # 키 개수 증가
        DiskWrite(x)  # 디스크에 쓰기
    
    # 만약 x가 리프 노드가 아니라면 (내부 노드)
    else:
        # 키 삽입 위치 찾기 (오른쪽에서 왼쪽으로 탐색)
        while i >= 1 and k < x.keys[i - 1]:
            i -= 1
        i += 1  # 적절한 자식으로 이동
        
        DiskRead(x.c[i - 1])  # 해당 자식을 읽음
        
        # 자식 노드가 가득 찼으면 분할
        if x.c[i - 1].n == (2 * t) - 1:
            BTreeSplitChild(x, i - 1)  # 자식 분할
            # 분할 후 키 비교 (중앙값 기준)
            if k > x.keys[i - 1]:
                i += 1
        
        # 재귀적으로 삽입 수행
        BTreeInsertNonFull(x.c[i - 1], k)

 

 

 

Split-Child 연산을 통해 재귀적으로 가득 찬 노드에 도달하지 않도록 보장했다.

자식 노드를 분할함으로써 항상 가득 차지 않은 노드로 탐색이 진행된다.

 

 

또한 Split-Child 연산을 사용하여 트리의 균형을 유지했다.

디스크 I/O가 핵심이기 때문에, 디스크 접근 횟수를 줄이는 것이 성능 최적화의 중요한 요소이다.

 

'cs > 데이터베이스' 카테고리의 다른 글

B-Tree 삭제 과정  (0) 2024.10.15
데이터베이스 저장에 왜 B-tree 자료구조가 필요할까?  (0) 2024.10.13
데이터베이스, 어떻게 설계하고 관리할까?  (5) 2024.10.12
데이터베이스와 DBMS의 기본적인 소개 및 특징  (3) 2024.10.12
cs/데이터베이스 관련 글
더 보기

티스토리툴바