All Pairs Shortest Paths (APSP) - Floyd-Warshall algorithm

All-Pairs Shortest Paths (APSP) 문제 정의

앞서 소개했던 Single-Source Shortest-Paths (SSSP)는 단일 vertex에서의 최단 경로 가중치와 정점을 구했었다.

이번엔 알아볼 APSP는 u에서 v로 가는 모든 정점 쌍 (u, v)를 찾는 방법이다.

 

 

방향이 있는 그래프 G(V, E)가 주어지면 edge의 가중치 함수를 실수 값으로 매핑하고, 해당 그래프를 행렬 W로 표현한다.

 

 

이와 같이 가중치 행렬 W가 주어지면

최단 경로 거리 행렬 D와, 최단 경로 선행 정점 행렬 Π를 계산한다.

 

 

 

 

 

APSP 문제 풀이 방법

 

저번에 배웠던 SSSP 알고리즘으로도 APSP 문제를 해결할 수 있다.

 

single souce이니만큼 당연하겠지만..

모든 정점을 출발점 source vertex로 설정하여 SSSP 알고리즘을 vertex의 수만큼 반복하면 된다.

 

 

음수 edge가 없는 그래프라면 Dijkstra's algorithm 으로 시간 복잡도는 O( V^2 logV + VE log V )이다.

밀집된 그래프라면 O(V^3 logV) 이다. (간선의 수 E = O(V^2) )

 

 

음수 edge가 있는 그래프라면 Bellman-Ford's algorithm 으로 시간 복잡도는 O(V^2 E) 이다.

밀집된 그래프라면 O(V^4) 이다. (간선의 수 E = O(V^2) )

 

 

이와 같이 SSSP로도 가능은 하지만 효율적인 면에서 한계가 있다.

 

이 문제를 조금 더 효율적으로 해결하기 위해 시간 복잡도를 O(V^3)로 줄일 수 있는 방법이 있다.

가장 짧은 edge의 개수는 4개

 

APSP 문제는 그래프의 두 정점 사이에서 최단 경로를 계산한다.

그래프에 ∣V∣ 개의 정점이 있을 때, 최단 경로 상에 있을 수 있는 최대 edge의 개수는 ∣V∣ -1 이므로 이를 초과할 수 없다.

 

 

단순하게 생각해보면 모든 경로를 하나씩 계산해볼 수 있다.

1개의 edge로 이루어진 모든 최단 경로를 계산하고, 2개의 edge, 3개... 이렇게 n - 1 개의 edge로 이루어진 모든 최단 경로를 계산할 수 있다. 하지만 너무 비효율적이다.

 

 

m개의 edge로 구성된 최단 경로를 어떻게 계산할 수 있을까

 

 

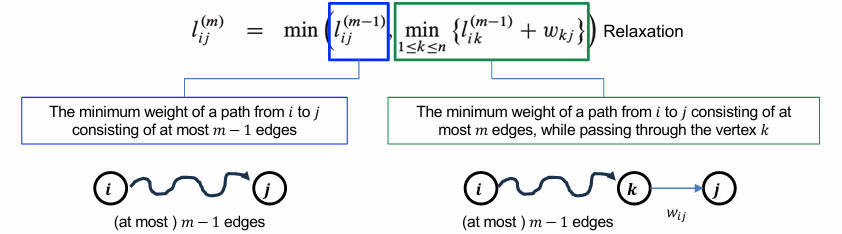
edge의 개수를 n X n 행렬 L(m)로 정의하자.

여기에서 각 원소 l(m)은 i 정점에서 j 정점까지의 경로 중, 최대 m개의 edge를 포함하는 경로의 최소 가중치를 말한다.

​따라서 L(1) = W이다. (W는 edge의 가중치 행렬)

 

 

각 원소 l의 첫 번째 항은 최대 m-1 개의 edge로 구성된 경로의 최소 가중치이다.

 

두 번째 항은 i에서 k를 거쳐서 최대 m-1개의 edge로 구성된 경로에
k에서 j로 가는 한 개의 edge를 추가하여 최대 m개의 edge로 구성된 최소 가중치이다.

 

이 개념은 Floyd-Warshall 알고리즘의 기초가 된다.

 

예를들어 이 그래프를 계산해보자.

 

길이 4인 vertex 3에서 5로 가는 원소 l35(4)​ = min( 11 , min(7−4, 4+7, 0+∞, 5+∞, 11+0) ) = min(11, 3, 11, ∞, 11) = 3 이다.

 

이 계산에서 L(4)는 L(3)과 W의 곱으로 나타낼 수 있으므로, 우리가 하려는 계산은 행렬곱과 비슷하다.

행렬곱을 이용해서 우리가 하려는 계산을 조금 더 단순화시킬 수 있다.

 

 

단순하게 행렬곱을 이용한 시간복잡도를 구해보자.

 

각 원소 l을 계산하는 데 O(V)의 시간이 소요되고, 이것을 V X V 행렬 L의 모든 원소에 대해 반복하므로 행렬L을 계산하는 데에만 필요한 시간은 O(V^2).

따라서 행렬 곱셈에 필요한 시간 복잡도는 O(V^3)이다.

 

행렬곱 O(V^3)을 V번 반복하여 L(V)까지 계산해야 하므로 전체 시간 복잡도는 O(V^4)가 된다.

 

이런 방식은 정확하지만 한계가 있고 효율적이지 않다.

APSP 문제를 해결하기 위한 효율적인 알고리즘으로 Floyd-Warshall 알고리즘이 있다.

 

 

 

 

 

Floyd-Warshall algorithm

 

Dynamic Programming 기반 APSP 알고리즘으로, 시간 복잡도는 O(V^3)이다.

음수 가중치가 있는 edge는 존재할 수 있지만 음수 cycle은 없어야 한다.

 

 

Floyd-Warshall 알고리즘은 최단 경로의 중간 정점(intermediate vertex)을 고려한다.

중간 정점들을 통해서 최단 경로를 계산한다.

 

 

 

Floyd-Warshall 알고리즘의 작동 원리는 다음과 같다.

 

1. 모든 정점 쌍 (i, j)에 대해 초기 경로 길이를 가중치로 초기화한다. 연결되지 않은 경우는 무한대로 설정.

d[i][j] = w[i][j] (직접 경로의 가중치) 또는 d[i][j] = ∞  (직접 경로가 없는 경우)

 

 

2. dp 적용

모든 정점 k를 중간 정점으로 고려하면서 최단 경로를 갱신한다.

d[i][j] = min( d[i][j], d[i][k] + d[k][j] )

이 과정은 정점 i에서 j로 가는 최단 경로가 k를 거쳐서 더 짧아질 수 있는지를 확인한다.

 

 

3. 최종 결과로 모든 정점 쌍에 대해 최단 경로 길이가 업데이트된 행렬을 얻는다.

 

 

 

2번에서 최단 경로 구조의 중간 정점을 고려하는 과정을 자세히 보자.

정점 i부터 j까지 모든 경로를 고려할 때, 경로의 중간 정점들이 집합 {v 1~k} 에서 모두 선택된다고 가정하자.

 

여기에서 경로 p를 i 에서 j로 가는 최단 경로라고 하고, d(k)ij 를 그 경로의 가중치라고 한다.

 

 

(1) 만약 정점 k가 경로 p의 중간 정점이 아닌 경우

경로 p의 모든 중간 정점은 집합 {v 1~ k-1}에 포함된다.

 

따라서 집합 {1 ~ k} 에서 모든 중간 정점이 선택된 경로의 가중치는 집합 {1 ~ k-1} 에서 모든 중간 정점이 선택된 경로의 가중치와 동일하므로, d(k)ij = d(k-1)ij 이다.

 

 

즉, 정점 k가 경로의 중간 정점이 아닌 경우 최단 경로의 가중치는 이전 단계에서 계산된 가중치와 같다.

 

 

 

(2) 만약 정점 k가 경로 p의 중간 정점인 경우

경로 p를 p1( i부터 k까지 )와 p2( k부터 j까지 )로 나눌 수 있다.

 

여기서 p1과 p2는 각각 최단경로이며, 이 경로들의 중간 정점은 모두 집합 {1 ~ k-1}에서 선택된다.

따라서 p1의 가중치는 d(k-1)ik 이고,  p2의 가중치는 d(k-1)kj 이다.

 

이에 대해서 모든 중간 정점이 선택된 최단 경로의 가중치는 d(k)ij = d(k-1)ik + d(k-1)kj 로 계산할 수 있다.

 

 

 

지금까지 설명한 것을 바탕으로, 우리는 최단 경로의 추정치를 재귀적인 방식의 공식으로 나타낼 수 있다.

 

이와 같은 방법은 시간 복잡도 O(1)로 표현할 수 있다.

 

각 행렬의 원소 l을 구했을 때, 시간복잡도 O(V)가 필요했던 경우와 비교된다.

 

 

 

Floyd-Warshall Algorithm의 슈도코드는 아래와 같다.

 

 

 

위 알고리즘에 따라 가중치와 선행자 행렬은 다음과 같은 과정으로 채워진다.