그래프 소개
그래프 G는 정점 V와 간선 E로 이루어져 있다.
정점 사이를 잇는 간선은 방향을 갖고 이어질 수도 있고, 방향 상관 없이 이어질 수도 있다.

각 그래프마다 노드가 갖는 차수 degree는
Undirected graph에서 edges의 수가 곧 차수이고,
directed graph에서는 incoming edges와 outgoing edges로 구분한다.
만약 그래프의 경로에서 모든 정점이 서로 다른 경우 경로가 simple하다고 말한다.
위 그래프에서 <2, 5, 4, 2> 같은 경우, 소스 정점을 제외한 cycle의 모든 정점은 simple하다.
반대로 사이클이 없는 경우 비순환 acyclic graph 라고 말한다.
그래프 표현 방법
Adjacency-matrix

그래프 |𝑉|×|𝑉|의 행렬 A[ i ][ j ] 는 해당 정점 i와 j 사이에 edge가 있으면 1로 표현한다.
방향이 없는 그래프의 경우, 주 대각선을 따라 대칭 행렬을 만든다.
이때, 행렬의 공간 복잡도는 O(V^2)
시간 복잡도는 행렬에 1로 표현된 간선의 수만큼 나타기 때문에
이웃 list는 O(|𝑉|)로 표현되고,
모든 edges의 list는 O(|𝑉|^2) 로 표현된다.
Adjacency-list

각 정점마다 하나씩 |𝑉| 의 배열 list를 나타낸다.
정점의 인접 list에는 인접한 정점이 포합된다.
인접 list의 공간 복잡도는 O( |𝑉| + |E| )
시간 복잡도는 vertex i의 차수로 표현되기 때문에
이웃 list는 O( degree of the vertex )로 표현되고,
모든 edges의 list는 O(E) 로 표현된다.
행렬과 리스트의 표현 방법 중 어떤 것이 더 낫다고 딱 말할 수 없다.
우리가 해결해야 할 문제 상황과 그래프의 밀도에 따라서 그때 그때 다르다.

Breath-first search (BFS)
그래프 G(V,E)와 소스 정점 s가 주어지면 G의 edge를 탐색하여 소스 s에서 도달 가능한 모든 정점을 발견한다.
s로부터 거리가 증가하는 순서(넓이 우선)으로 정점을 발견한다.
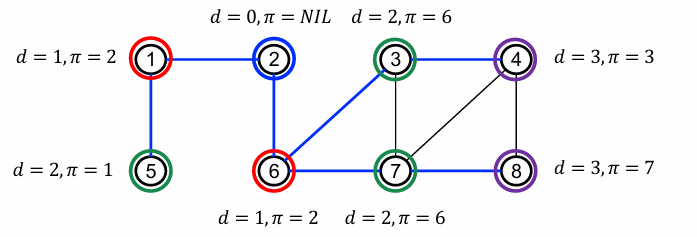
정점 u로부터 v까지의 거리는 이 정점까지 가는 데에 필요한 가장 짧은 경로의 edges들의 숫자로 계산한다.
우선, 거리 1에 있는 모든 정점을 검색한 후, 거리 2에 있는 순서로 검색을 늘려간다.

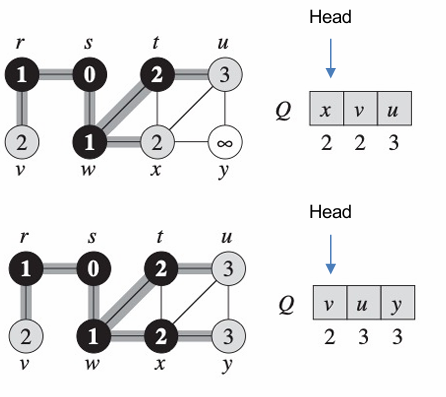
위 알고리즘에 따라 BFS를 진행하면 다음과 같은 큐의 상태를 확인할 수 있다.

여기에서 각 정점의 색깔이 의미하는 것은 다음과 같다.
흰색: 발견되지 않음(enqueue)
회색: 발견되었으나 완료되지 않음(여전히 Q에 있음)
검정색: 완료됨(dequeue)
과정 예시
BFS의 시간 복잡도를 구해보면,
각 정점은 최대 한 번만 검사하고
각 edge는 최대 두 번 탐색되므로
알고리즘의 초기화 부분은 O( |𝑉| )
탐색 부분은 O( |𝑉| + |E| ) 이다.

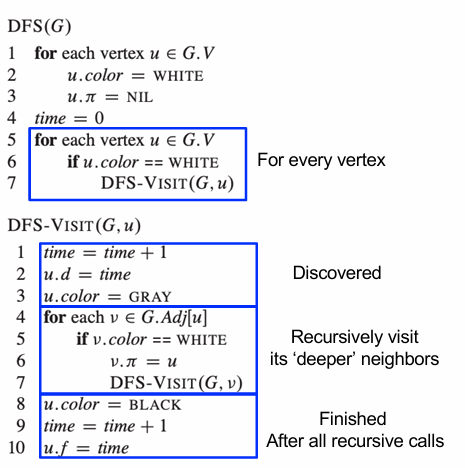
Depth-first search (DFS)
그래프에서 너비가 아닌, 깊이 위주의 검색을 한다.
DFS에서는 각 정점 v에 두 개의 타임 스탬프
발견시간 v.d( 발견 시 I가 회색으로 변함 )과, 완료시간 v.f( v가 검정색으로 변할 때 )이 있다.
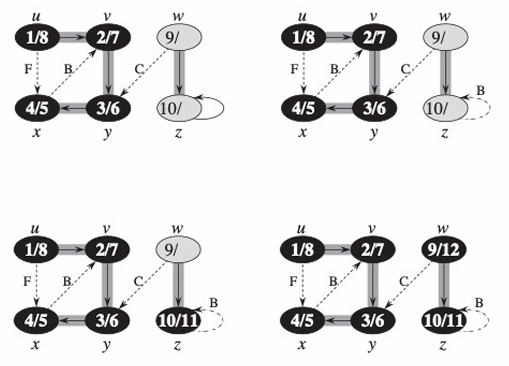
DFS 그래프의 과정
DFS 알고리즘의 시간 복잡도는 초기화 부분에서 O( |𝑉| )
탐색 부분은 O( |𝑉| + |E| ) 이다.