허프만 코드 소개
허프만 코드는 greedy 접근 방식을 기반으로 한 데이터 압축 방식이다.
그러면 어떻게 데이터를 압축하는지 방법을 알아보자.
우선 임의의 문자열을 각각의 문자로 구분해둔다.
그리고 각 문자의 빈도와 그 문자를 이진수로 구분하기 위한 binary character code를 표시한다.

여기에서 fixed length는 위에서 주어진 6개의 문자를 나타내기 위해 항상 3개의 고정된 비트가 필요하다는 의미이다.
위와 같이 설정한 경우, 필요한 메모리 공간은
( 45,000 + 13,000 +12,000+16,000+9,000+5,000) ∗ 3 으로, 30만 비트가 필요하다.
이와 같은 방법을 개선하기 위해서 우리는
빈도가 높은 문자에는 크기가 작은 이진수를, 빈도가 낮은 문자에는 크기가 큰 이진수를 부여하는 방법을 생각해볼 수 있다.
개선점 Variable-length code
앞서 설명한 fixed-length code와 반대되는 개념으로, 문자의 빈도에 따라 각각 다른 길이의 이진 코드를 사용하는 것이다.

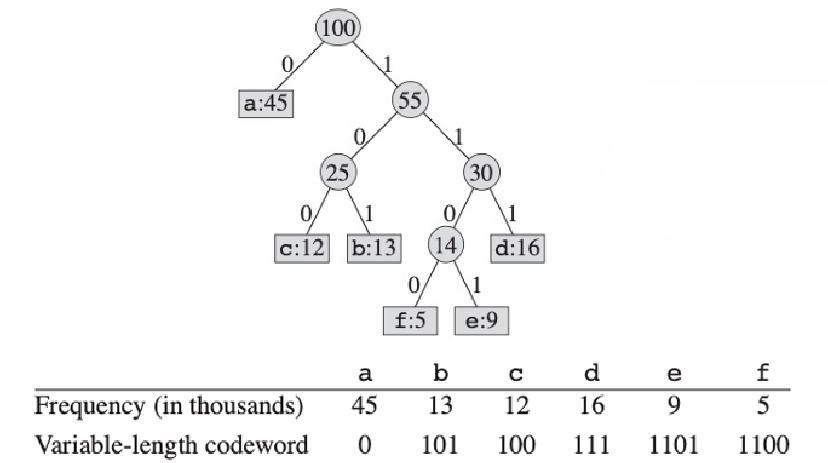
위 예시 처럼 가장 높은 빈도를 갖는 문자 a에 가장 짧은 길이의 코드를 부여한 것을 볼 수 있다.
그렇다면, 이와 같이 설명한 경우 메모리 공간은
( 45 ,000 ∗ 1+13,000∗3 + 12,000∗3 + 16,000∗3 + 9,000∗4 + 5,000∗4 ) = 22만4천 비트이다.
이러한 방법만으로 메모리 공간을 25% 절약할 수 있었다.
Prefix code
그런데 예를들어 문자 a를 0, b를 01, c를 1이라고 설정했을 때
001을 decoding 하게 된다면 이것은 aac로 해석해야 할까, ab로 해석해야할까 애매한 경우가 있다.
이때 a의 코드 0은 b 코드 01의 prefix라고 한다.
이런 문제를 해결하기 위해서 어떤 코드 단어도 다른 코드 단어의 접두사가 되지 않는 코드를 Prefix Codes로 설정한다.
즉, 한 코드 단어가 다른 코드 단어의 접두사( Prefix )가 되지 않게 해야 한다.
예를 들면

여기에서 각각의 코드 단어들은 다른 코드들의 접두사가 될 수 없다.
만약에 001011101을 해석해야 한다고 하면,
0 + 0 + 101 + 1101 라는 조합으로 유일한 경우의 수인 aabe로 decoding할 수 있다.
이런 Prefix code의 특징 덕분에, 특정 코드 단어가 나왔을 때 그것이 유일하게 해석될 수 있다는 것을 보장할 수 있다.
위에서 설명한 prefix code의 특징은 이진 트리의 root에서 leaf node까지의 단순 경로로 해석될 수 있다.
여기에서 각각의 leaf는 각 문자에 해당한다.
fixed-length code는 모든 리프 노드가 마지막 레벨에 배치되는 이진 트리로 표현될 수 있다.
이 중, 3비트 고정 길이 코드로 예를 든 것은 다음과 같다.

variable-length code는 리프 노드가 서로 다른 레벨에 배치되는 full binary tree로 표현될 수 있다.
codewords tree의 비용
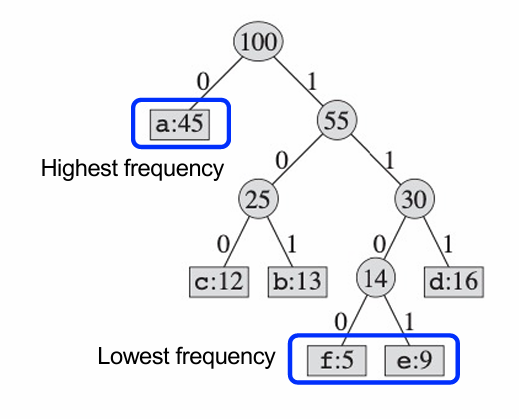
파일에 대한 최적의 코드는 항상 full binary tree로 표현된다.
이 트리는 문자가 자주 나타날수록 루트에 가까운 leaf에 배치되어야 한다.
그리고, 임의의 C라는 문자 집합에 대한 full binary tree는 leaf node |C|와 internal node |C‑1|를 갖는다.
트리의 비용을 T라고 했을 때, B(T)를 파일을 인코딩하는 데에 필요한 비트 수 라고 하자.
이 때 성립하는 공식은 다음과 같다.

여기에서 c.freq는 문자 c에 대한 빈도를 의미하고,
d(c) 는 c에 대한 코드워드의 길이, 즉 루트에서 리프 노드까지의 거리를 말한다.
우리의 목표는 비용 B(T)를 최소화하는 full binary tree를 구성하는 것이다.
비용을 최소화하기 위해 최적의 prefix code에 대한 full binary tree를 구성하는 방법론을 알아보자.
optimal prefix code methodology ( 그리디 알고리즘의 방법론 )
greedy 알고리즘을 사용하여 최적의 prefix code에 대한 full binary tree를 구성하는 방법을 알아보자.

leaf node |C| 에서 시작하고 |C-1| 을 합치는 연산을 수행한다.
문자들의 집합 C의 완전 이진 트리는 |C| leaf node 들과 |C-1| 내부 노드들을 갖는다.
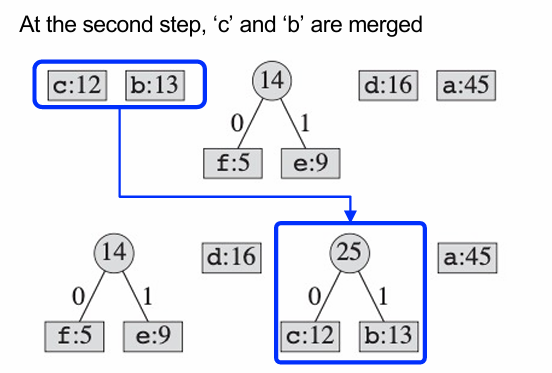
여기서 greedy한 선택은 가장 빈도가 낮은 문자 두개를 합치는 것이다.
문자는 빈도가 가장 낮은 두 문자를 식별하기 위해 min-priority queue Q에 저장된다.
우선, 방금 말했듯이 가장 빈도가 낮은 두 문자를 합친다.

두 내부 노드를 합쳐서 새로운 노드를 생성할 때는 내부 노드의 빈도 수의 합을 넣는다.
위와 같은 과정을 반복한다.
여기서도 가장 적은 수의 빈도를 갖는 14와 16을 합쳐서 새로운 트리로 만들어준다.

25와 30을 합치고

마지막 노드까지 합쳐서 완전 이진 트리를 완성해준다.

시간복잡도 분석

여기에서 파란색은 HeapSort의 Build min heap 부분에 대응하여 O(n)이다.
빨간 부분과 녹색 부분은 각각 Merge와 Min-Heapify에 대응하므로 O(n log n)이다.
따라서 total 시간 복잡도는 O(n log n)이다.
Correctness (허프만 코드의 정확도)
여기에서 정확도가 의미하는 것은, 우리가 얻은것이 최적의 prefix code인가를 묻는다.
즉, 우리가 얻은 솔루션이 optimal한가를 판단한다.
이것을 판단하는 방법에는 두 가지가 있다.
Greedy-choice property
x와 y를 가장 낮은 빈도를 갖는 두 문자라고 하자.
그 때, x와 y의 길이가 같고 마지막 비트만 다른 최적의 prefix code가 존재한다.
이 때 greedy한 선택에 tree를 구성하는 최소한의 비용을 갖는 최적의 solution이 포함된다.

아까 완성한 완전 이진 트리에서 e와 f 문자를 보면 codeword의 길이가 같고 마지막 비트만 다른 것을 확인할 수 있다.
이와 같은 아이디어는 임의의 optimal한 prefix code tree T를 선택하고,
문자 x와 y가 last level에서 형제 leaf들로 나타나는 또다른 최적의 prefix code tree로 표현되는 트리를 만들기 위하여 T를 수정한다.

Optimal substructure
x와 y를 가장 낮은 빈도를 갖는 C와 C' = 𝐶− {𝑥, 𝑦} ∪ {𝑧} 라고 하자.
여기에서 x, y, z는 각 문자의 빈도를 나타낸다.
다음으로, T' 를 C' 에 대한 최적의 prefix code tree 라고 설정하자.
그럼 C에 대한 최적의 prefix code tree T는
문자 x와 y를 갖는 leaf node z를 대체하는 것으로
T' 로부터 얻을 수 있다.


