DP - LCS (Longest Common Subsequence)

Longest Common Subsequence (가장 긴 공통 부분 수열)

LCS는 수열 X와 Y가 주어졌을 때, 이 두 개의 수열에서 순서가 서로 같은 부분을 찾는 문제이다.

예를들어 수열 X가 <BCDB>일때 Y<ABCBDAB> 에서 LCS는 ABCBDAB 이다.

이런 문제는 DNA같은 생물학적 분야에 응용하여 적용될 수 있다.

예를들어 DNA 분자 구성이 주어지고
X = ACCGGTCGAGTGCGCGGAAGCCGGCCGAA
Y = GTCGTTCGGAATGCCGTTGCTCTGTAAA
일때 X와 Y 중 DNA와 더 비슷한 수열을 찾는 경우가 있다.

DP로 풀기 위해서는 일단 main problem을 작은 subproblem으로 쪼개야 한다.

우선 순열을 식별하자. (특징 잡기)

순열 X에 prefix i를 붙여서 i개의 개수만큼만 나열한다.
예를 들어 순열 X=<A,B,C,B,D,A,B> 라고 할때, X2 = <A,B> X4 = <A,B,C,B>

더 작은 수준의 subproblem으로 만들어보자.

우리는 순열 Xm과 Yn을 입력해서 새로운 LCS 순열 Zk를 만들것이다.

경우를 나눠보자.

1. 만약 Xm과 Yn이 같다면, Zk도 같을 것이고, Zk-1은 Xm-1과 Yn-1의 LCS일 것이다.

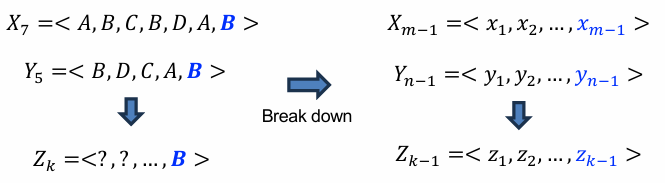
만약 Xm과 Yn이 서로 다르다면, 다시 두 가지 경우로 나뉜다.
Zk는 Xm이랑 다를 수도 있고, Yn이랑 다를 수도 있다.

그러면 Z는 Xm-1과 Y의 LCS이거나, X와 Yn-1의 LCS이다.

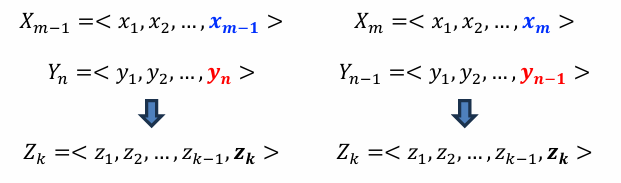
이렇게 이전 분석을 바탕으로 반복을 최적해로 표현할 수 있다. 최적해를 표 tabulation에 기록하자.

위 알고리즘을 슈도코드로 표현하면 아래와 같다.

우선 순열 X와 Y의 요소를 하나씩 비교해 나간다.

만약 두 문자가 같다면 이전 요소 c[i-1,j-1]에 +1 을 한 것을 저장한다.

다르다면 c[i-1,j] 와 c[i,j-1] 중 큰 값을 저장한다.

여기에서 서로 다를 때, c[i-1,j] 와 c[i,j-1] 중 큰 값을 저장해서 표를 채우는 것은
전체 수열 중에서 공통으로 이어지는 부분과, 끊어졌다가 다시 이어지는 부분에서 다시 lcs의 길이를 이어가기 위함이다.

LCS 테이블을 통해 이전까지 계산했던 공통 순열 부분을 다시 계산하지 않고,

이전 i-1행 이나 j-1열 값을 바로 불러와서 효율적으로 재사용할 수 있다.

위 과정으로 최대 몇 개의 문자열의 순서가 공통으로 이어지는지 개수를 알 수 있었다.

그러면 이제 아까 작성한 테이블을 기반으로 공통되는 문자열을 찾아보자.

우선 우리가 구한 LCS 테이블의 마지막 값에서부터 시작한다.

이 값의 왼쪽, 혹은 위쪽 ( c[i-1,j] 와 c[i,j-1] ) 값과 현재 값을 비교한다.
같은 값이 있으면 그 요소로 이동하고, 없다면 out 배열에 해당 문자를 넣고 c[i-1,j-1]로 이동한다.

위 알고리즘에서는 c[i-1,j] >= c[i,j-1] 이기 때문에 위쪽으로 이동할 것이다.

끝에서부터 배열에 입력해왔으므로, 0으로 이동해서 마지막 문자를 넣었다면 out 배열의 순서를 뒤집어준다.

LCS의 시간 복잡도는 subproblem을 구하는 데 m과 n번 반복하니 O(mn),

공간 복잡도는 저장할 table이 b와 c가 있으니 O(mn)이 된다.

학교 강의 및 벨로그 정리